Solving One-Step Linear Equations: Multiplying & Dividing
Purplemath
We've seen that numbers can be added to and subtracted from variables. When this is the case, we undo the addition with subtraction, and undo the subtraction with addition. But what if numbers are multiplied on or divided into a variable?
The "undo" of multiplication is division. If something is multiplied on the x, we can undo it by dividing both sides of the equation (that is, by dividing each term on either side side of the "equals" sign) by whatever is multiplied on the x. The process looks like this:
Content Continues Below
-
Solve 2x = 5
The variable is the letter on the left-hand side (LHS) of the equation. The variable is multiplied by two.
I want the x to stand alone on one side of the equation. Since the x is multiplied by 2, I need to divide on both sides by 2, in order to get the variable by itself. This is called "dividing through by 2", and it looks like this:
Then the solution is:
Advertisement
Note: The fractional form, as displayed above, is the preferred form for answers. Unless you're told to use the decimal form, or unless the equation started out with numbers having decimal places (rather than numbers which are integers or fractions), you should expect to need to use the fractional forms for your answers.
Yes, plugging things into your calculator and copying down the decimal approximation or decimal equivalent can indeed get your answer counted as "wrong", at least in part. If in doubt, check with your instructor before the next test.
The "undo" of division is multiplication. So, if the variable is divided by something, the one-step solution is to multiply through by that something (that is, to multiply both sides of the equation by the denominator of the fraction that's with the variable); that is, you'll want to multiply through in order to "clear" the denominator(s) and solve the equation.
-
Solve
The variable is on the left-hand side. It's not by itself; it's divided by five. Since the x is divided by 5, I'll want to multiply both sides by 5. This gives me:
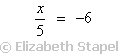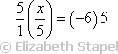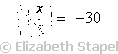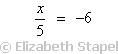
x/5 = −6
(5/1)(x/5) = (−6)(5)
![]()
x = −30
The above solution is animated on the "live" page.
Then the solution is:
x = −30
In the process of solving (displayed above in the animation), I multiplied by 5 on the right-hand side of the equation, and by on the left-hand side. Since , I was multiplying both sides by the same thing, even though they didn't look exactly alike.
But why did I do it? I did it because it is often easier to keep track of what I'm doing, when working with fractions, if all the numbers involved in a given computation are in fractional form. Since I was needing to cancel a which was, in effect, multiplied against the variable on the left-hand side, it was useful to multiply by 5 in the form ; this allowed me to cancel off the denominator, while keeping track of what I was doing. Most students find this habit to be helpful, so try to cultivate it now.
Content Continues Below
Remember what we discussed earlier: The solution to an equation is the value that makes the equation "true". This fact allows us to check our solutions. All we have to do is plug those solution values back into the original equations, and confirm that we end up with true statements. (Or, if we don't, we know it's time to check our work!)
The first equation above was 2x = 5, and my solution was . To verify that this solution value is correct, I can plug the numerical value back in to the original equation, in place of the variable, and see if it works:
-
Check whether is a solution for the equation 2x = 5
To check to see if the value they've given me solves the equation, I'll plug the number, , in for the variable x in the equation. I'll then simplify, and make sure that the value on the left-hand side (LHS) of the equation is the same as the value on the right-hand side (RHS) of the equation.
Checking:
The left-hand side, after evaluating it at , came out to be the same value as the right-hand side. This means that the proposed solution value, , is indeed a valid solution to the equation.
When you have an exercise where you're told to check a solution (or to "verify" it, or whatever), the "answer" to such an exercise is to show the checking, like I did above. If you plug in the solution value, and you end up with a true statement, then the solution "checks". But if you do the plug-n-chug on scratch-paper or in your calculator, and do not include it (neatly!) in your hand-in work, don't expect to receive many (or any) points. You must show your work on the "check".
When you're in the section on solving linear equations and you're told to check if a given value is a solution, pretty much always the given value will be the solution to the given equations. But not always.
-
Check whether x = 1 is a solution for 2x = 5
To check the solution, I'll plug it into the original equation, in place of the variable on the left-hand side (LHS). If the LHS simplifies to equal the right-hand side (RHS), then the proposed solution is correct. If not, then it isn't.
Checking:
LHS: 2(1) = 2
RHS: 5
LHS ≠ RHS
It's always possible that the solution didn't "check" because I made a mistake somewhere, but I've double-checked, and my work is right. Then I notice that this is the first exercise I did at the top of this page. From that, I know that the solution is actually , not x = 1.
By showing that the two sides of the original equation are no longer equal if I let x = 1, I have proved that x = 1 is not a solution to the equation. Then my answer is:
not a solution
Affiliate
While "not a solution" is "the answer" to the above exercise, the credit comes from having shown that the two sides of the original equation evaluate to different values. If you are given an exercise of this type, don't expect to get credit if your answer is nothing more than "is a solution" or "is not a solution". You must show the check.
Affiliate
-
Solve , and check your solution.
In this equation, the variable is divided by a three. Well, I'll actually call it a negative three, because I want the x by itself, which will include getting rid of the "minus" sign.
To get the x by itself, I need to undo the current division. The undo of division is multiplication, so I'll multiply both sides of the equation (that is, I'll "multiply through") by −3. This will "clear the denominator".
Now I need to check my answer, to make sure that it works.
Checking:
Since both sides of the equation simplify to the same value, I know that my solution is correct.
For my hand-in work, the above confirmation is the "check" that they want. And I'll put my numerical solution at the end of my work:
x = −12
You may have questions about how the "minus" sign was handled in the previous exercise. Don't forget that we can view a "minus" on a term as being multiplication on that term by a −1, and it doesn't matter if we multiply or divide by a −1; the resulting sign and value will be the same. So what I'd done in my head was:
Then I'd multiplied through by the −3 to get rid of the denominator on the LHS of the equation.
Being flexible in this manner will prove very helpful to you throughout your studies. Make sure you're comfortable with "minus" signs!
-
Solve 2 = −x
This is the same exercise as what we'd seen on the previous page, but this time I'm studying how to solve one-step equations with multiplication and division. So they're probably expecting me to solve this by multiplying or dividing. But how? All there is on the variable is a "minus" sign.
Ah, but then I remember that this "minus" can be regarded as a −1, so the equation they've given me can be written as:
2 = (−1)(x)
To solve this, I can divide both side by (that is, "divide through by") −1:
This is the same answer as I got last time.
x = −2
There is one "special case" related to the "undoing multiplication" case above:
When the variable (x or whatever) is multiplied by a fraction, we can "undo" this multiplication by dividing both sides of the equation by that fraction. But, to divide by a fraction, we flip that fraction and multiply. In other words, in order to isolate a variable that is multiplied by a fraction, we just multiply both sides of the equation by the flip (that is, by the "reciprocal") of that fraction.
-
Solve , and check your solution.
Since x is multiplied by the fraction , I'll want to multiply both sides by the flip of this fraction, being . This will cancel off the fraction currently multiplied on the variable x.
(Note: Many students find it helpful to also turn the 10 on the right-hand side of the equation into a fraction also, by putting it over 1, so it's easier to see what multiplies and what divides.)
To check my solution, I'll plug it back in for the variable in the original equation, and make sure that the two sides of the equation simplify to the same value:
Checking:
So my solution checks, and my answer is:
You can use the Mathway widget below to practice solving a linear equation by multiplying or dividing. Try the entered exercise, or type in your own exercise. Then click the button to compare your answer to Mathway's. (Or skip the widget and continue with the lesson.)
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
URL: https://www.purplemath.com/modules/solvelin2.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()



