Number Bases: Octal and Hexadecimal
Purplemath
Octal
An older computer-based number system is "octal", or base eight. The digits in octal math are 0, 1, 2, 3, 4, 5, 6, and 7. The value "eight" is written as "1 eight and 0 ones", or 108.
In technical terms, there are very many different computer-language protocols for octal, but we'll just be using the simple mathematical system.
Content Continues Below
A few New-World tribes used base-8 numbering systems; they counted by using the eight spaces between their fingers, rather than the ten fingers themselves. The blue natives in the movie "Avatar" used octal because their hands had only four fingers.
Let's dig right in:
-
Convert 35710 to the corresponding base-eight number.
I will do the usual sequential division, this time dividing by 8 at each step:
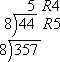
Once I got to the "5" on top, I had to stop, because 8 doesn't divide into 5.
Then the corresponding octal number is 5458.
-
Convert 5458 to the corresponding decimal number.
I will follow the usual procedure, listing the digits in one row and then counting off the digits from the RIGHT in the next row, starting at zero:
digits: |
5 |
4 |
5 |
numbering: |
2 |
1 |
0 |
Then I'll do the usual addition and multiplication:
5×82 + 4×81 + 5×80
= 5×64 + 4×8 + 5×1
= 320 + 32 + 5
= 357
Then the corresponding decimal number is 35710.
Hexadecimal
If you work with computer programming or computer engineering (or computer graphics, about which more later), you will encounter base-sixteen, or hexadecimal, math.
Affiliate
Advertisement
As mentioned before, decimal math does not have one single solitary digit that represents the value of "ten". Instead, we use two digits, a 1 and a 0: "10". But in hexadecimal math, the columns stand for multiples of sixteen! That is, the first column stands for how many units you have, the second column stands for how many sixteens, the third column stands for how many two hundred fifty-sixes (sixteen-times-sixteens), and so forth.
In base ten, we had digits 0 through 9. In base eight, we had digits 0 through 7. In base 4, we had digits 0 through 3. In any base system, you will have digits 0 through one-less-than-your-base. This means that, in hexadecimal, we need to have "digits" 0 through 15. To do this, we would need single solitary digits that stand for the values of "ten", "eleven", "twelve", "thirteen", "fourteen", and "fifteen". But we don't. So, instead, we use letters. That is, counting in hexadecimal, the sixteen "numerals" are:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
In other words, A is "ten" in "regular" numbers, B is "eleven", C is "twelve", D is "thirteen", E is "fourteen", and "F" is fifteen. It is this use of letters for digits that makes hexadecimal numbers look so odd at first. But the conversions work in the usual manner.
-
Convert 35710 to the corresponding hexadecimal number.
Here, I will divide repeatedly by 16, keeping track of the remainders as I go. (You might want to use some scratch paper for this.)
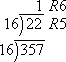
Reading off the digits, starting from the top and wrapping around the right-hand side, I see that:
35710 = 16516.
-
Convert 16516 to the corresponding decimal number.
List the digits, and count them off from the RIGHT, starting with zero:
digits: |
1 |
6 |
5 |
numbering: |
2 |
1 |
0 |
Remember that each digit in the hexadecimal number represents how many copies you need of that power of sixteen, and convert the number to decimal:
1×162 + 6×161 + 5×160
= 1×256 + 6×16 + 5×1
= 256 + 96 + 5
= 357
Then 16516 = 35710.
Content Continues Below
-
Convert 6393310 to the corresponding hexadecimal number.
I will divide repeatedly by 16, keeping track of my remainders:
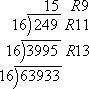
From the sequential division above, I can see that the hexadecimal number will have a "fifteen" in the sixteen-cubeds column, a "nine" in the sixteen-squareds column, an "eleven" in the sixteens column, and a "thirteen" in the ones column. But I cannot write the hexadecimal number as "1591113", because this would be confusing and imprecise. So I will use the letters for the "digits" that are otherwise too large, letting "F" stand in for "fifteen", "B" stand in for "eleven", and "D" stand in for "thirteen".
Then 6393310 = F9BD16.
-
Convert F9BD to decimal notation.
I will list out the digits, and count them off from the RIGHT, starting at zero:
digits: |
F |
9 |
B |
D |
numbering: |
3 |
2 |
1 |
0 |
Actually, it will probably be helpful to redo this, converting the alphabetic hexadecimal "digits" to their corresponding "regular" decimal values:
digits: |
15 |
9 |
11 |
13 |
numbering: |
3 |
2 |
1 |
0 |
Now I'll do the multiplication and addition:
15×163 + 9×162 + 11×161 + 13×160
= 15×4096 + 9×256 + 11×16 + 13×1
= 61440 + 2304 + 176 + 13
= 63933
As expected, F9BD16 = 6393310.
Computer Graphics
If you work on web pages and graphics programs, you may find it helpful to convert between the RGB values (for an image in your graphics program) and the hexadecimal values (for a matching background color on the web page).
Affiliate
Graphics programs deal with the RGB (red-green-blue) values for colors. Each of these components of a given color have values somewhere between 0 and 255. These values may be converted to hexadecimal values between 00 and FF. If you list the RGB components of a color as a string of three numbers, you might get, say, R:204, G:51, B:255, which translates into a light-purplish #CC33FF in HTML coding. Note that 20410 = CC16, 5110 = 3316, and 25510 = FF16.
On the other hand, if you have some coding for #990033, this would translate into a dark-reddish R:153, G:0, B:51 in your graphics program. That is, to convert between your graphics program and your web-page coding, deal with the hexadecimal number not as one six-digit number, but as three two-digit numbers, and convert these pairs of digits into the corresponding RGB values.
For a discussion of the history of "web safe" colors, including why they involve only the hexadecimal equivalents of 0, 51, 102, 153, 204, and 255, look here. For a demonstration of the different text and background colors in HTML, look here.
URL: https://www.purplemath.com/modules/numbbase3.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




