Number Bases: Base 4 and Base 7
Purplemath
Base 4
In base four, each digit in a number represents the number of copies of that power of four. That is, the first digit tells you how many ones you have; the second tells you how many fours you have; the third tells you how many sixteens (that is, how many four-times-fours) you have; the fourth tells you how many sixty-fours (that is, how many four-times-four-times-fours) you have; and so on.
Content Continues Below
The methodology for conversion between decimal and base-four numbers is just like that for converting between decimals and binaries, except that binary digits can be only "0" or "1", while the digits for base-four numbers can be "0", "1", "2", or "3".
(As you might expect, there is no single solitary digit in base-four math that represents the quantity "four".)
-
Convert 35710 to the corresponding base-four number.
I will do the same division that I did before for binaries, keeping track of the remainders. (You may want to use scratch paper for this.)
Naturally, since this is base-4, I'll be dividing by 4s.
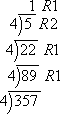
Then 35710 converts to 112114.
-
Convert 80710 to the corresponding base-four number.
I'll divide again by 4s.
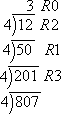
Note: Once I got to that "3" on top, I had to stop, because four cannot divide into 3.
Reading the numbers off the division, I see that 80710 converts to 302134.
-
Convert 302134 to the corresponding decimal number.
I will list out the digits, and then number them from the RIGHT, starting at zero:
digits: |
3 |
0 |
2 |
1 |
3 |
numbering: |
4 |
3 |
2 |
1 |
0 |
Each digit stands for the number of copies I need for that power of four:
3×44 + 0×43 + 2×42 + 1×41 + 3×40
= 3×256 + 0×64 + 2×16 + 1×4 + 3×1
= 768 + 32 + 4 + 3
= 807
As expected, 302134 converts to 80710.
Content Continues Below
Base Seven
I can't think of any particular use for base-seven numbers, but they will serve us by providing some more practice with conversions.
-
Convert 35710 to the corresponding base-seven number.
I do the division, this time by 7s:
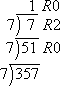
Then 35710 = 10207.
-
Convert 1334610 to the corresponding base-seven number.
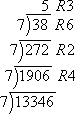
When I got to that "5" on top, I had to stop, because 7 can't divide into 5.
Then 1334610 = 536247.
-
Convert 536247 to the corresponding decimal number.
I will list the digits, and count them off from the RIGHT, starting at zero:
digits: |
5 |
3 |
6 |
2 |
4 |
numbering: |
4 |
3 |
2 |
1 |
0 |
Then I'll do the multiplication and addition:
5×74 + 3×73 + 6×72 + 2×71 + 4×70
= 5×2401 + 3×343 + 6×49 + 2×7 + 4×1
= 12005 + 1029 + 294 + 14 + 4
= 13346
Then 536247 = 1334610.
URL: https://www.purplemath.com/modules/numbbase2.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()



