Venn Diagrams: Set Notation
Purplemath
In addition to working with generic sets (the plain A, B, and C from the previous examples) and their relationships, you may be asked to work with specific sets, using Venn diagrams to find new sets.
-
Given that U = {1, 2, ..., 9, 10}, A = {1, 2, 3, 4, 5, 6}, B = {2, 4, 6, 8, 9}, and C = {3, 5, 6, 7, 9}, populate a Venn diagram and use this to find [(A − C) B].
My first step is to draw the diagram.
Content Continues Below
Since they've given me three sets inside the universe, I'll draw three circles inside a box, and label them with the sets' names.
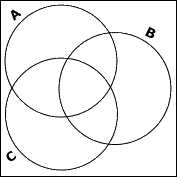
(They don't usually want the universe named; the box is sufficient indication. For some reason, the names on the circles whose elements are given go outside the circles, which can be confusing. Despite the drawing, there are no elements A, B, or C in this universe.)
Affiliate
The set A contains the numbers 1, 2, 3, 4, 5, and 6. (These numbers are the set's elements.) The number 6 is in all three of the input sets, so this element will go in the triangle-ish central overlap area of all three circles. Also, A shares 2 and 4 with B, so these will go in the rest of the overlap of these two sets. And A shares 3 and 5 with C, so this will go in the rest of the overlap area with C. The remaining elements, being in this case just the number 1, go into the only-A part of A's circle.
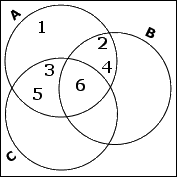
The set B shares 6 and 9 with C. (I've already handled its overlap with A.) But 6 is shared by all three sets, so I only need to put the 9 in the overlap with C. The remaining elements, being in this case just the number 8, go into the only-B part of B's circle.
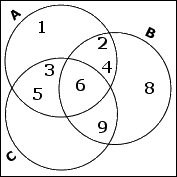
The set C is left and, since I've already handled the overlaps with A and B, I only need to insert the remaining elements of C, which is just the number 7. This go in the only-C portion of C's circle.
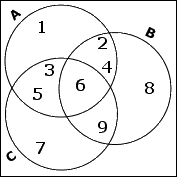
There is one number which isn't in any of the named sets. So, outside of the circles, I'll put the remaining 10.
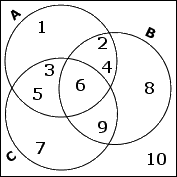
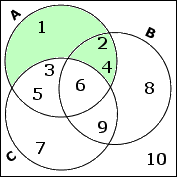
I've completed the "population" portion of this exercise. To handle the set relationships, I'll work from the inside out. I need first to find A complement C, which is A, after I've thrown out its overlap with C. This gives me:
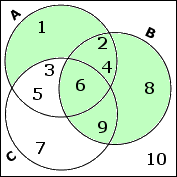
Now I have to add in all of B:
And now I have to take the complement of this, which means that I'll flip the shading, giving me something that includes most of C and the otherwise unclaimed portion of U:
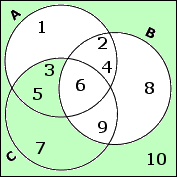
From this diagram, I can read off the new set created by the set-relation expression they gave me:
Content Continues Below
While Venn diagrams are commonly used for set intersections, unions, and complements, they can also be used to show subsets.
For instance, the picture below displays that A is a subset of B:
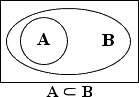
As you can see above, a subset is a set which is entirely contained within another set. For instance, every set in a Venn diagram is a subset of that diagram's universe.
Venn diagrams can also demonstrate "disjoint" sets. In the graphic below, A and B are disjoint:
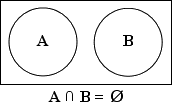
That is, disjoint sets have no overlap; their intersection is empty. There is a special notation for this "empty set", by the way: "Ø".
Affiliate
(Unless you have an odd computer set-up, the preceding character looks like an "O" with a forward slash through it. If you're on a PC, you can type this "empty set" character by holding down the "ALT" key and typing "0216" on the numeric keypad.)
This "Ø" character is pronounced as "the empty set".
Affiliate
An illustration of a use of these set relationships would be the manner in which some search engines process searches:
- If you type "cats AND dogs" into the search box, a search engine using this syntax (called "Boolean" logic) will return all web pages that contain both the word "cats" and the word "dogs". This corresponds to the set " C D".
- If, on the other hand, you type "cats OR dogs", the search engine will return web pages that contain either the word "cats" or the word "dog" (or both, because the mathematical meaning of "or" is "inclusive"). This "or" statement corresponds to the set " C D".
- If you type "cats NOT dogs", the search engine will return pages containing the word "cats", but only after discarding all the pages which also contain the word "dogs". This corresponds to the set " C − D".
URL: https://www.purplemath.com/modules/venndiag3.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()



