Return to the Purplemath home page

 

Return to the Lessons Index  | Do the Lessons in Order  |  Print-friendly page

Systems of Non-Linear Equations:
     Intermediate-Difficulty Systems (page 4 of 6)

Need a personal math teacher?

The non-linear systems we've solved so far have been one quadratic equation and one linear equation, which graphed as a parabola and a straight line, respectively. Moving up in difficulty, we come to solving systems of two quadratic equations, which will graph as two parabolas; and similarly messy systems.

  • Solve the following system:

    • y = 2x2 + 3x + 4
    y = x2 + 2x + 3

    As before, I'll set these equations equal, and solve for the values of x:

      

    2x2 + 3x + 4 = x2 + 2x + 3
    x2 + x + 1 = 0

    Using the Quadratic Formula:

      

      

      

      
    x = (-1 sqrt(-3))/2

    But I can't graph that negative inside the square root! What's going on here?

    Take a look at the graph:

      

      

      

      

      

      

      

      

      
    graph of system

    The lines do not intersect. Since there is no intersection, then there is no solution. That is, this is an inconsistent system. My final answer is: no solution: inconsistent system.

Advertisement

In general, the method of solution for general systems of equations is to solve one of the equations (you choose which) for one of the variables (again, you choose which). Then you plug the resulting expression into the other equation for the chosen variable, and solve for the values of the other variable. Then you plug those solutions back into the first equation, and solve for the values of the first variable. Here are some additional examples:  Copyright 2002-2011 Elizabeth Stapel All Rights Reserved

  • Solve the following system:

      • y = x 3
      x2 + y2 = 17

    Graphically, this system is a straight line (from the first equation) crossing a circle centered at the origin (from the second equation):

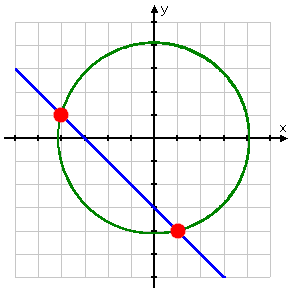
      graph of y = -x - 3 and x^2 + y^2 = 17

    There appear to be two solutions. I'll proceed algebraically to confirm this impression, and to get the exact values.

    Since the first equation is already solved for y, I will plug "x 3" in for "y" in the second equation, and solve for the values of x:

      x2 + y2 = 17
      x2 + (x 3)      2 = 17
      x2 + (x 3)(x 3) = 17
      x2 + (x2 + 6x + 9) = 17
      2x2 + 6x + 9 = 17
      2x2 + 6x 8 = 0
      x2 + 3x 4 = 0
      (x + 4)(x 1) = 0
      x = 4, x = 1

    When x = 4,  y = x 3 = (4) 3 = 4 3 = 1

    When x = 1,  y = x 3 = (1) 3 = 4

    Then the solution consists of the points (4, 1) and (1, 4).

Note the procedure: I solved one of the equations (the first equation looked easier) for one of the variables (solving for "y=" looked easier), and then plugged the resulting expression back into the other equation. This gave me one equation in one variable (the variable happened to be x), and a one-variable equation is something I know how to solve. Once I had the solution values for x, I back-solved for the corresponding y-values. I emphasize "corresponding" because you have to keep track of which y-value goes with which x-value. In the example above, the points (4, 4) and (1, 1) are not solutions. Even though I came up with x = 4 and 1 and y = 4 and 1, the x = 4 did not go with the y = 4, and the x = 1 did not go with the y = 1.

Warning: You must match the x-values and y-values correctly. Be careful!

Content Continues Below

  • Solve the following system of equations:

      • y = (1/2)x 5
      y = x2 + 2x 15

    Since both equations are already solved for y, I'll set them equal and solve for the values of x:

      (1/2)x 5 = x2 + 2x 15
          x 10 = 2x2 + 4x 30
                  0 = 2x2 + 3x 20
                  0 = (2x 5)(x + 4)

      x = 5/2, x = 4

    When x = 5/2:

      y = (1/2)x 5 = (1/2)(5/2) 5 = 5/4 20/4 = 15/4 = 3.75

    When x = 4:

      y = (1/2)x 5 = (1/2)(4) 5 = 2 5 = 7

    Then the solutions are the points ( 5/2, 15/4 ) and (4, 7).

Graphically, the above system looks like this:

 

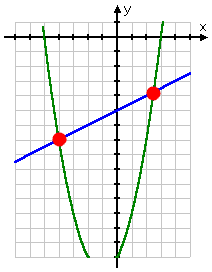
The intersection points on the graph appear to be good matches for the numerical solutions I got via algebra, confirming that I've done the exercise correctly.

graph of y = (1/2)x - 5 and y = x^2 + 2x - 15
 

  • Solve the following system of equations:

      • xy = 1
      x + y = 2

    Taking a quick look at the graph, I see that there appears to be only one solution:

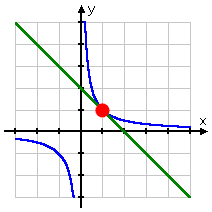
      graph of xy = 1 and x + y = 2

    I guess I'll solve the second equation for y, and plug the result into the first equation:

      x + y = 2
      y = x + 2

    Then:

      xy = 1
      x(x + 2) = 1
      x2 + 2x = 1
      x2 + 2x 1 = 0
      x2 2x + 1 = 0
      (x 1)(x 1) = 0
      x = 1

    Then:

      x + y = 2
      (1) + y = 2
      y = 1

    Then the solution is the point (1, 1).

<< Previous  Top  |  1 | 2 | 3 | 4 | 5 | 6  |  Return to Index  Next >>

Cite this article as:

Stapel, Elizabeth. "Systems of Non-Linear Equations: Intermediate Systems." Purplemath.
    Available from https://www.purplemath.com/modules/syseqgen4.htm.
    Accessed
 

 

Purplemath:

Linking to this site
School licensing

The "Homework
   Guidelines"

Study Skills Survey

Find a local math tutor

  Copyright 2002-2012  Elizabeth Stapel   |   About   |   Terms of Use

 

Contact Us