Symmetry and Graphs
Purplemath
Symmetry is more of a geometrical than an algebraic concept but, as mentioned in the previous two pages, the subject of symmetry does come up in a couple of algebraic contexts. When you're graphing quadratics, you may be asked for the parabola's axis of symmetry. This is usually just the vertical line x = h, where "h" is the x-coordinate of the vertex, (h, k). That is, a parabola's axis of symmetry is usually just the vertical line through its vertex. The other customary context for symmetry is judging from a graph whether a function is even or odd.
Note: By definition, no function can be symmetric about the x-axis (or any other horizontal line), since anything that is mirrored around a horizontal line will violate the Vertical Line Test.
Content Continues Below
On the other hand, a function can be symmetric about a vertical line or about a point. In particular, a function that is symmetric about the y-axis is also an "even" function, and a function that is symmetric about the origin is also an "odd" function. Because of this correspondence between the symmetry of the graph and the evenness or oddness of the function, "symmetry" in algebra is usually going to apply to the y-axis and to the origin.
-
In what follows, list any symmetries, if any, for the displayed graph, and state whether the graph shows a function.
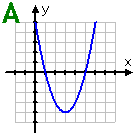
Graph A: This graph is symmetric about its axis; that is, it is symmetric about the line x = 3. There is no other symmetry. This graph shows a function.
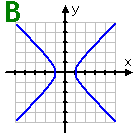
Graph B: This graph is symmetric about the axes; that is, it is symmetric about the lines x = 0 (the y-axis) and y = 0 (the x-axis). It is also symmetric about the origin. Since there exist vertical lines (such as the line x = 2) which will cross this graph twice, what it shows is not a function.
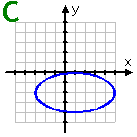
Graph C: This graph is symmetric about the lines x = 1 and y = −2, and symmetric about the point (1, −2). Since a vertical line can be drawn to cross the ellipse twice, this is not a function.
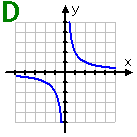
Graph D: This graph is symmetric about slanty lines: y = x and y = −x. It is also symmetric about the origin. Because this hyperbola is angled correctly (so that no vertical line can cross the graph more than once), the graph shows a function.
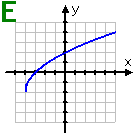
Graph E: This graph (of a square-root function) shows no symmetry whatsoever, but it is a function.
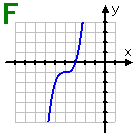
Graph F: This graph (of a cubic function) is symmetric about the point (−4, −1), but not around any lines. This graph does show a function.
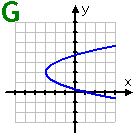
Graph G: This parabola is lying on its side. It is symmetric about the line y = 2. It is not a function.
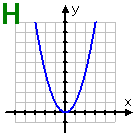
Graph H: This parabola is vertical, and is symmetric about the y-axis. It is a function; in fact, it is an even function.
Content Continues Below
-
In what follows, determine from the graphs whether the displayed functions are even, odd, or neither.
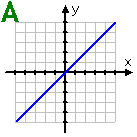
Graph A: This linear graph goes through the origin. If I rotate the graph 180° around the origin, I'll get the same picture. So this graph is odd. (The function would not be odd if this line didn't go through the origin.)
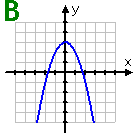
Graph B: This parabola's vertex is on the y-axis, so the axis of symmetry is the y-axis. That means that the function is even.
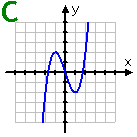
Graph C: This cubic is centered on the origin. If I rotate the graph 180° around the origin, I'll get the same picture. So this graph is odd.
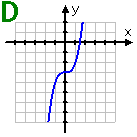
Graph D: This cubic is centered at the point (0, −3). This graph is symmetric, but not about the origin or the y-axis. So this function is neither even nor odd.
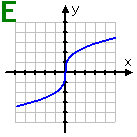
Graph E: This cube root is centered on the origin, so this function is odd.
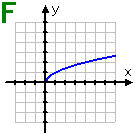
Graph F: This square root has no symmetry. The function is neither even nor odd.
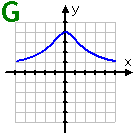
Graph G: This graph looks like a bell-shaped curve. Since it is mirrored around the y-axis, the function is even.
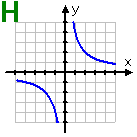
Graph H: This hyperbola is symmetric about the lines y = x and y = −x, but this tells me nothing about evenness or oddness. However, the graph is also symmetric about the origin, so this function is odd.
Affiliate
Affiliate
When looking for symmetry, you don't have to just sit there trying the puzzle the thing out in your head. Instead, take the paper and your pencil, and see if there is a spot where you can plant the pencil's eraser, and then spin the paper on the table. When it's spun halfway around, do you get the same picture as you had before? Then your eraser marks a point of symmetry. Grab a ruler and stand it on its edge in the middle of the graph. Look down onto the paper, and eye-ball the two "sides" of the picture. Do the two portions of the graph, one on either side of the ruler, look like mirror images? Then the ruler marks a line of symmetry. Don't be shy about putting your hands into the work; it can really help in getting a "feel" for symmetry.
Affiliate
URL: https://www.purplemath.com/modules/symmetry3.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()