Solving Simple Radical Equations
Purplemath
We'll start with a couple simple exercises. As we go, remember that we must square the two sides of an equation, rather than the individual terms in those two sides. And when the instructions for an exercise say to check one's answers, this means that you need to show your check as part of your hand-in work.
If the instructions don't tell you that you must check your answers, check them anyway. At the very least, compare your solution with a graph on your graphing calculator.
Content Continues Below
-
Solve the equation, and check.
On the left-hand side of this equation, I have a square root. By definition, this is positive. On the right-hand side, I've got a positive number. Since both sides are known positive, squaring won't introduce extraneous solutions. But I'll check my solution at the end, anyway, because the instructions require it.
First, I'll square both sides of the equation they've given me:
x − 2 = 25
x = 27
Now, I need to show my check of this solution. When I plug 27 in for x in the left-hand side of the original equation, does the result simplify to the original right-hand side, "5"?
My solution checks, so my answer is:
x = 27
Affiliate
-
Solve the equation, and check your answer.
The left-hand side of this equation is a square root. By definition, this will be positive. The right-hand side of the equation will sometimes be positive and sometimes be negative.
Affiliate
Because of this fact, my squaring of both sides of the equation will be an irreversible step. So I'd have been checking my solutions for this question, even if they hadn't told me to.
I'll treat the two sides of this equation as two functions, and graph them, so I have some idea what to expect. (I won't draw the graph or hand it is. This is for my own sense of confidence in my work.) I'll graph the two sides of the equation as:
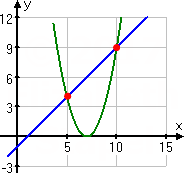
![y_1 = sqrt[x − 1] is blue arc, y_2 = x − 7 is green diagonal line; a red dot at (x, y) = (10, 3) marks the intersection point](radicals/solve17.gif)
The intersection point looks to be around x = 10, so I'll expect my solution to be at least close to that value.
To solve the equation properly (that is, algebraically), I'll start by squaring each side of the original equation:
x − 1 = (x − 7)(x − 7)
x − 1 = x2 − 14x + 49
This is just a quadratic equation, which is easy to solve:
x − 1 = x2 − 14x + 49
0 = x2 − 15x + 50
0 = (x − 5)(x − 10)
x = 5, 10
I'd expected the x = 10 solution. Where did that other solution come from?
It came from my squaring both sides of the original equation. The squaring created an extraneous solution. I can see it in the squared functions and their graph:
y1 = x − 1
y2 = x2 − 14x + 49
("Extraneous", pronounced as "eck-STRAY-nee-uss", in this context means "mathematically correct, but not relevant or useful, as far as the original question is concerned". If the term hasn't come up in your class yet, you should expect to hear it shortly.)
Affiliate
By squaring both sides, I created an extra (and wrong) solution. Now I'll prove which solution is right by checking my answers. My check is done by plugging the proposed solution into both the left-hand side (LHS) and right-hand side (RHS) of the original equation, and confirming that each simplifies to the same value (or else showing that the solution isn't any good):
x = 5:
So x = 5 is not a valid solution.
x = 10:
So x = 10 is a valid solution, and my answer is:
x = 10
Even if the instructions hadn't told me to check my answers, clearly I needed to. And I needed to do that check with algebra, not with the picture. Yes, the picture can be extremely helpful, but it isn't proof. Expect to receive only partial credit if you discard an apparent solution without showing why you've done so.
Content Continues Below
-
Solve
Square both sides:
25 − x2 = 16
9 = x2
±3 = x
I have two possible solutions. The instructions didn't say to check them, but I'm going to, to be on the safe side:
x = −3:
RHS: 4
RHS = LHS
So this solution works. What about the other one?
x = 3:
RHS: 4
RHS = LHS
So both solutions are valid, and my answer is:
x = ±3
Yes, sometimes you'll get more than one solution for a particular equation, and they'll all be valid.
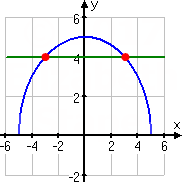
This is why we check all solutions to radical equations, and use graphs to help us be sure of our results.
URL: https://www.purplemath.com/modules/solverad2.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()