General Quadratic Word Problems
Purplemath
Most quadratic word problems should seem very familiar, as they are built from the linear problems that you've done in the past. You will need to use keywords to interpret the English and, from that, create the quadratic model. Then solve the model for the solutions (that is, the x-intercepts).
Content Continues Below
When interpreted — within the context of the exercise — one or both of the solutions to the quadratic equation will provide at least part of the answer they've asked of you.
Advertisement
- A picture has a height that is 4/3 its width. It is to be enlarged to have an area of 192 square inches. What will be the dimensions of the enlargement?
The height is defined in terms of the width, so I'll pick a variable for "width", and then create an expression for the height.
Let "w" stand for the width of the picture. The height h is given as being 4/3 of the width, so:
h = (4/3)w
Then the area, being the product of the width and the height, is given by:
A = hw
= [(4/3)w][w]
= (4/3)w2 = 192
Affiliate
I need to solve this "area" equation for the value of the width, and then back-solve to find the value of the height.
(4/3)w2 = 192
w2 = 144
w = ± 12
Since I can't have a negative width, I can ignore the "w = −12" solution. Then the width must be the other solution, 12, and the height is then:
h = (4/3)(12) = 16
I can do a quick check of my answer, since this is a "solving" exercise, by plugging my values back into the original exercise. Since 12 × 16 does indeed equal 192, my answer checks. So my hand-in answer is:
The enlargement will be 12 inches by 16 inches.
- The product of two consecutive negative integers is 1122. What are the numbers?
Remember that consecutive integers are one unit apart, so my numbers are n and n + 1. Multiplying to get the product, I get:
n(n + 1) = 1122
n2 + n = 1122
n2 + n − 1122 = 0
(n + 34)(n − 33) = 0
The solutions are n = −34 and n = 33. I need a negative value (because the exercise statement specified that the numbers are negative), so I'll ignore the n = 33& and take n = −34. Then the other number is:
n + 1 = (−34) + 1 = −33
Then my hand-in answer is:
The two numbers are −33 and −34.
Note that the second value could have been gotten by changing the sign on the extraneous solution. Warning: Many students get in the very bad habit of arbitrarily changing signs to get the answers they need, but this does not always work, and will very likely get them in trouble later on. (And it'll cause trouble right now, if the grader is paying attention.)
Take the extra half a second to find the right answer the right way.
Content Continues Below
- A garden measuring 12 meters by 16 meters is to have a pedestrian pathway installed all around it, increasing the total area to 285 square meters. What will be the width of the pathway?
The first thing I need to do is draw a picture. Since I don't know how wide the path will be, I'll label the width as "x".

Looking at my picture, I see that the total width of the finished garden-plus-path area will be:
x + 12 + x = 12 + 2x
...and the total length will be:
x + 16 + x = 16 + 2x
Then the new area, being the product of the new width and height, is given by:
(12 + 2x)(16 + 2x) = 285
192 + 56x + 4x2 = 285
4x2 + 56x − 93 = 0
This quadratic is messy enough that I won't bother with trying to use factoring to solve; I'll just go straight to the Quadratic Formula:
Obviously the negative value won't work in this context, so I'll ignore it. Checking the original exercise to verify what I'm being asked to find, I notice that I need to have units on my answer:
The width of the pathway will be 1.5 meters.
- You have to make a square-bottomed, unlidded box with a height of three inches and a volume of approximately 42 cubic inches. You will be taking a piece of cardboard, cutting three-inch squares from each corner, scoring between the corners, and folding up the edges. What should be the dimensions of the cardboard, to the nearest quarter inch?
When dealing with geometric sorts of word problems, it is usually helpful to draw a picture. Since I'll be cutting equal-sized squares out of all of the corners, and since the box will have a square bottom, I know I'll be starting with a square piece of cardboard.
I don't know how big the cardboard will be yet, so I'll label the sides as having length "w".

Since I know I'll be cutting out three-by-three squares to get sides that are three inches high, I can mark that on my drawing.
The dashed (rather than solid) lines show where I'll be scoring the cardboard and folding up the sides.
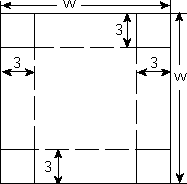
Since I'll be losing three inches on either end of the cardboard when I fold up the sides, the final width of the bottom will be the original "w" inches, less three on the one side and another three on the other side. That is, the width of the bottom will be:
w − 3 − 3 = w − 6
The volume will be the product of the width, the length (which is the same as the width), and the depth (which was created by cutting out the corners and folding up the sides).
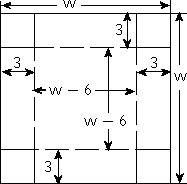
Then the volume of the box, working from the drawing, gives me the following equation:
(w − 6)(w − 6)(3) = 42
(w − 6)(w − 6) = 14
(w − 6)2 = 14
This is the quadratic I need to solve. I can take the square root of either side, and then add the to the right-hand side:
...or I can multiply out the square and apply the Quadratic Formula:
w2 − 12w + 36 = 14
w2 − 12w + 22 = 0
Affiliate
Either way, I get two solutions which, when expressed in practical decimal terms, tell me that the width of the original cardboard is either about 2.26 inches or else about 9.74 inches.
How do I know which solution value for the width is right? By checking each value in the original word problem.
If the cardboard is only 2.26 inches wide, then how on earth would I be able to fold up three-inch-deep sides? But if the cardboard is 9.74 inches, then I can fold up three inches of cardboard on either side, and still be left with 3.74 inches in the middle. Checking:
(3.74)(3.74)(3) = 41.9628
This isn't exactly 42, but, taking round-off error into account, it's close enough that I can trust that I have the correct value. So my hand-in answer, complete with units, is:
The cardboard should measure 9.75 inches on a side.
In this last exercise above, you should notice that each solution method (factoring and the Quadratic Formula) gave the same final answer for the cardboard's width. But the Quadratic Formula took longer and provided me with more opportunities to make mistakes.
Moral? Don't get stuck in the rut of always using the Quadratic Formula.
URL: https://www.purplemath.com/modules/quadprob2.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




