Return to the Purplemath home page

 

Return to the Lessons Index  | Do the Lessons in Order  |  Print-friendly page

Quadrants and Angles (page 3 of 3)

Sections: Introduction, Worked Examples (and Sign Chart), More Examples

  • Find the values of the remaining trigometric ratios if
    tan(alpha) = sqrt[7] / 3 and     sin(α) < 0.

    • The tangent is positive in QI and in QIII. The sine ratio is negative in QIII and QIV. The overlap is QIII, so α must terminate in the third quadrant. In the third quadrant, each of x and y is negative, so the numerator and denominator of the tangent ratio y/x are both negative.

     

    I'll draw what I've got so far:

    The Pythagorean Theorem gives me:

     

    axes drawn, terminal side of (alpha) in QIII, height y = -sqrt[7], base x = -3

      (sqrt[7])^2 + 3^2 = 7 + 9 = 16 = r^2, so r = +/- 4

    The hypotenuse r is always positive, so
    r = +4 and now my picture becomes:

     

     

     

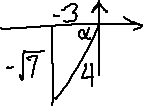
    same right triangle, but with hypotenuse labelled as r = 4

    Then the other ratios are:

      sin(alpha) = -sqrt[7]/4, cos(alpha) = -3/4, csc(alpha) = -4/sqrt[7], sec(alpha) = -4/3, cot(alpha) = -3/sqrt[7]

The answers for the cosecant and cotangent can be expressed in either of two ways, depending on whether your particular text book still cares whether you leave radicals in the denominator. Your calculus book probably won't care; your algebra book definitely did care; trig books vary. If you're not sure what is the protocol for your class, ask your instructor.

  • The equation 5x + 3y = 0, x < 0, is the equation of the terminal side of an angle alpha. Find the values of the six trigonometric ratios for this angle.

    • This is an unusual sort of exercise, but I can use what I've learned in algebra to pick it apart. First, I'll solve for "y=" to get the equation y = –(5/3)x. From what I remember of graphing, this is an decreasing line through the origin, so it passes through QII and QIV. Since they gave me the restriction that x is negative, then the angle alpha must end in QII.

     

     

    So I've got this much so far:

     

    axis system, with y = -(5/3)x drawn, but only in QII; point (-3, 5) is labelled

     

      Copyright © Elizabeth Stapel 2010-2011 All Rights Reserved

    Dropping the perpendicular to create the right triangle, I can label the side lengths from the point, and also label the angle, to get:

     

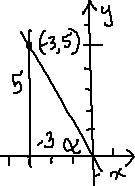
    perpendicular added between (-3, 5) and x-axis; height y = 5, base x = -3

    The height is y = 5 and the base is x = –3, so the hypotenuse is given by:

      52 + (–3)2 = r2
      25 + 9 = r2
      34 = r2
      +/- sqrt[34] = r

    Since r is always positive, then r = sqrt[34], so my triangle is:

     

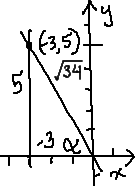
    same triangle and axis system, but with r = 6 added to triangle's labelling

    Then the six trig ratios are:

      sin(alpha) = 5/sqrt[34], cos(alpha) = -3/sqrt[34], tan(alpha) = -5/3, csc(alpha) = sqrt[34]/5, sec(alpha) = -sqrt[34]/3, cot(alpha) = -3/5

<< Previous  Top  |  1 | 2 | 3  |  Return to Index

Cite this article as:

Stapel, Elizabeth. "Quadrants and Angles: More Examples." Purplemath. Available from
    https://www.purplemath.com/modules/quadangs3.htm. Accessed
 

 

Purplemath:
  Linking to this site
  Printing pages
  School licensing

Reviews of
Internet Sites:
   Free Help
   Practice
   Et Cetera

The "Homework
   Guidelines"

Study Skills Survey

Tutoring from Purplemath
Find a local math tutor

  Copyright © 2010-2012  Elizabeth Stapel   |   About   |   Terms of Use

 

Contact Us