Is the Inverse Also a Function?
Defs / Inverting a GraphFinding InversesRestricted DomainsWorked ExamplesQuarter-CirclesProving Inverses
Purplemath
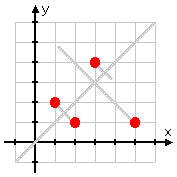
Suppose you are given a function which is the following set of points:
{ (1, 2), (2, 1), (3, 4), (5, 1) }
The inverse of this function is the same set of points, but the x's and y's have been reversed:
{ (2, 1), (1, 2), (4, 3), (1, 5) }
Content Continues Below
This inverse has two points, (1, 2) and (1, 5), that share a common x-value but have different y-values. This means that the inverse is NOT a function.
Graphically, the original function looks like this:

You can find the inverse algebraically, by flipping the x- and y-coordinates, or graphically, by drawing the line y = x...
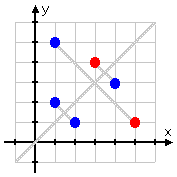
...and reflecting all the points across it:
Affiliate
(It's perfectly okay for the inverse to overwrite the original function's points. The points (2, 1) and (1, 2) of the inverse overwrote the points (1, 2) and (2, 1) of the original function, which is why two red dots went missing when we did the inverse. But this sharing of points between function and inverse is totally okay.)
So the inverse of the original relation is the blue dots in this graphic:
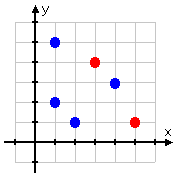
However, you can see from the graph above that the inverse is not a function. This is because there are two points in the inverse that are sharing an x-value. The inverse fails the Vertical Line Test:

There is a quick way to tell, before going to the trouble of finding the inverse, whether the inverse of a function will itself be a function. You've seen that you sort of "flip" the original function over the line y = x to get the inverse. Using this fact, someone noticed that you can also "flip over" the Vertical Line Test to get the Horizontal Line Test.
Content Continues Below
What is the Horizontal Line Test?
The Horizontal Line Test allows you to check, from the graph of a function, whether that function's inverse will also be a function. If there is any place on the graph of the original function where a horizontal line would cross two more more times, then the inverse of that function will not itself be a function. If all horizontal lines cross at most one spot on the original graph, then the inverse will be a function, too.
As you can see, we can draw a horizontal line through two of the points in the original function (being the original set of points):
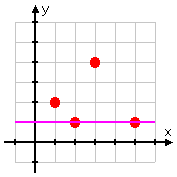
Advertisement
Since the original function had two points that shared the same Y-VALUE, then the inverse of the original function will not be a function.
Affiliate
This means, by the way, that no parabola (that is, no graph of a quadratic function) will have an inverse that is also a function.
In general, if a function's graph does not pass the Horizontal Line Test, then the graphed function's inverse will not itself be a function; if the list of points contains two or more points having the same y-coordinate, then the listing of points for the inverse will have two or more points having the same x-value and thus will not be a function.
So when you're asked, "Will the inverse be a function?" and you're given a graph, draw a horizontal line; if you're given a list of points, compare the y-coordinates.
What is the purpose of inverse functions?
The inverse of a function is helpful for when you want to work backwards, but not have to solve an equation over and over. For instance, suppose you have a function that models some situation (say, you plug in how much time you've worked and the function spits out how much you get paid) and you want to go backwards (in this example, by plugging in how much you'd like to get paid and finding how many hours you'd need to work). Instead of plugging in a y-value and solving the original formula for the input x-value, you can work directly with the inverse function's formula.
what is an example of an inverse function in real life?
One example of an inverse function in real life is the formula for converting between temperature scales. If you want to convert degree Celcius (°C) into degrees Fahrenheit (°F), you can plug the Celcius temperature into this formula:
But if you're wanting to convert the temperatures in the other direction (cuz, say, you're an American and want to figure out how Australia's summer temperatures compare to those in your own area), you'd either have to plug a Fahrenheit temperature into the above formula and then solve for the corresponding Celcius temperature, or else you can simply use the inverse function:
The inverse function is easier and quicker to use, compared to back-solving over and over again in the original function.
URL: https://www.purplemath.com/modules/invrsfcn2.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()