Solving Quadratic Inequalities
Purplemath
How do you solve quadratic inequalities?
To solve a quadratic inequality, you follow these steps:
- Get the quadratic on one side of the inequality symbol, so you're left with just zero on the other side.
- Find the zeroes of the associated quadratic equation (by factoring or applying the Quadratic Formula).
- Use these zeroes to split the number line into intervals.
- Pick the solution intervals by using the test-point method (annoying), the factor method (overkill for quadratics), or the parabola method (which you can instantly do in your head).
Content Continues Below
In the first example below, I will demonstrate all three solution methods. By the time I'm done, I think you'll agree that the one method that they *never* teach is by far the simplest and speediest.
- Solve x2 − 3x + 2 > 0
Affiliate
Advertisement
Working through the steps (listed above) for solving this quadratic inequality, my first step is to get the quadratic on one side of the inequality symbol, with zero on the other side. Since that's how they formatted the inequality they gave me, this step is already done. I have a quadratic for which I need to find the interval(s) where it is greater than zero.
Now I have to find the x-intercepts of the associated quadratic equation, because the intercepts are where x2 − 3x + 2 = 0 is equal to zero. These zeroes split the number line into intervals, of which one or another may be a solution interval. So I need to find where the associated quadratic equation crosses, or at least touches, the x-axis.
Factoring the quadratic, I get:
x2 − 3x + 2 = 0
(x − 2), (x − 1) = 0
x = 1 or x = 2
Then the graph crosses the x-axis at 1 and at 2, and the number line is divided into the following intervals:
(−∞, 1), (1, 2), (2, +∞)
Between the x-intercepts, the graph is either above the axis (and thus positive, or greater than zero), or else below the axis (and thus negative, or less than zero).
There are three algebraic ways of checking for this positivity or negativity on the intervals. I'll show all three.
Affiliate
1) Test-point method. The intervals between the x-intercepts are (−∞, 1), (1, 2), and (2, +∞). I will pick a point (any point) inside each interval. I will use that point to test the value of the quadratic at that point. Whatever turns out to be the sign on the quadratic at this test point, that is the sign or the quadratic for that entire interval.
For the (−∞, 1) interval, let's say I choose x = 0 as my test point. I plug this value into the quadratic and simplify to find the value and, more importantly, the sign on that value:
0 − 0 + 2 = 2
So my result is a positive value. This tells me that the quadratic is positive on the whole interval of (−∞, 1). Therefore, this interval is thus part of the solution, since I'm looking for a "greater than zero" solution.
For the interval (1, 2), I'll pick, say, x = 1.5. Then I get:
(1.5)2 − 3(1.5) + 2
= 2.25 − 4.5 + 2
= 4.25 − 4.5
= −0.25
This value is negative, which means that the quadratic is negative on this entire interval. Because I'm looking for positive values (because this is an "or greater than zero" inequality), this interval can not be part of the solution.
For the interval (2, +∞), I'll pick, say, x = 3. Plugging this value into the quadratic, I get:
(3)2 − 3(3) + 2
= 9 − 9 + 2 = 2
This value is positive, so this interval is another part of the solution.
Then the complete solution for the inequality is:
x < 1 or x > 2
(Why "or"? Because x cannot be less than 1 and also, at the same time, be greater than 2.)
2) Factor method. The factor method relies on factoring the quadratic (assuming that it does indeed factor), finding the signs of each factor on each interval, and then multiplying these signs to find the sign of the complete quadratic on that interval.
I already did the factoring (above), so my factors are:
(x − 2), (x − 1)
Now I will consider each of these factors separately.
The factor x − 1 is positive for x > 1; similarly, x − 2 is positive for x > 2. Thinking back to when I first learned about negative numbers, I know that (plus)×(plus) = (plus), (minus)×(minus) = (plus), and (minus)×(plus) = (minus). So, to compute the sign on y = x2 − 3x + 2, I only really need to know the signs on the factors. Then I can apply what I know about multiplying negatives.
First, I set up a grid, showing the number line, the factors, and the intervals into which the zeroes of those factors divide the number line.

Next, I mark the intervals where each factor is positive with a "plus" sign.
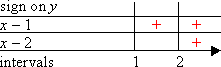
Where the factors aren't positive, they must be negative. So I mark the remaining slots with "minus" signs.
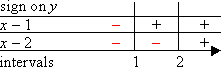
Now I multiply up the columns, to compute the sign of the complete quadratic on each interval.
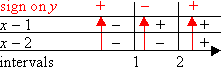
Then the solution of x2 − 3x + 2 > 0 are the two intervals with the "plus" signs:
(−∞, 1) or (2, +∞).
3) Parabola method. They gave me a quadratic and asked me where it was positive. Graphically, this means that they asked me where the quadratic's parabola was above the x-axis. Because the quadratic was positive (that is, because the leading coefficient was a *plus* 1), I know that its parabola must be above the axis at either end. It is only in the middle, between the two zeroes, that the parabola will dip below the axis.
So all I have to do is find the zeroes of the quadratic, and then pick the two intervals on the ends, rejecting the interval in the middle.
I already have the factors and the zeroes (from my initial work above):
x = 2, x = 1
Picturing the right-side up parabola in my head, I can see that my solution is:
x < 1 or x > 2
Can ya kinda see why I like the parabola method the best? It's *so* way easier! (The factor method, though, will come in handy for much more complicated inequalities, so please don't dismiss it entirely.)
Content Continues Below
How can inequality solutions be formatted?
There are different formats for inequality solutions. Using the exercise above, the solution can be formatted as:
- inequality notation:
x < 1, x > 2 - set notation:
{x | x < 1, x > 2} - interval notation:
(−∞, 1) ∪ (2, +∞) - number line with parentheses/brackets:
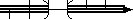
- number line with open/closed dots:
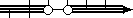
The particular solution format you use will depend on your text, your teacher, and your taste. Each format is equally valid.
- Solve −2x2 + 5x + 12 ≤ 0
First I find the zeroes, which will be the endpoints of my intervals:
−2x2 + 5x + 12 = 0
(−2x − 3)(x − 4) = 0
So the endpoints of the intervals will be at and 4. The intervals are between these endpoints, so my intervals are:
(Note that I have used brackets, rather than parentheses, for the endpoints in this "or equal to" inequality, because the endpoints *will* be included in the final solution.)
To find the intervals where y is negative by the Test-Point Method, I just pick a point in each interval. I can use points such as x = −2, x = 0, and x = 5. But that's time-consuming.
To find the intervals by the Factor Method, I solve each factor, fill out the grid, and multiply to get my result:
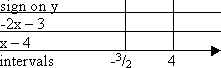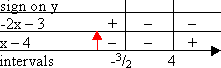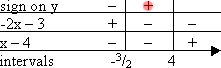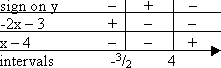
But that's overkill.
Instead, I'll use the parabola method. They want to know where a negative quadratic (that is, an upside-down parabola) is negative (that is, is below the x-axis). That's easy: on the intervals at the ends; the parabola will be above the axis in the middle, so that's the interval that I discard.
Then the solution to this inequality is all x's in:
Don't assume, based on the above two examples, that you'll always be wanting the two intervals on the ends for your solution. You'll sometimes want the middle interval, just one point, no part of the number line at all, or the whole number line.
- Solve x2 < x + 12
Unlike the exercises above, this one has given me an inequality where I first have to isolate the quadratic. So I'll do that first, by subtracting the x and the 12 over to the left-hand side:
x2 < x + 12
x2 − x − 12 = 0
This inequality is asking me to find the interval(s) on which a positive quadratic (which graphs as a right-side up parabola) is negative (that is, is below the x-axis). That's easy: picturing the parabola in my head, I see that the solution will be the interval between the two zeroes. So all I have to do is find the zeroes and pick the interval between them:
x2 − x − 12 = 0
(x + 3)(x − 4) = 0
x = −3, 4
Using the parabola method, I can go directly from my zeroes to my solution:
(−3, 4)
- Solve x2 + 4 ≤ 4x
My first step is to isolate the quadratic, which I'll do by subtracting the 4x over to the left-hand side of the inequality. Then I'll find the zeroes of the quadratic, so I can set up my intervals.
x2 + 4 ≤ 4x
x2 − 4x + 4 = 0
(x − 2)(x − 2) = 0
x = 2
So I have only one distinct zero, which means that the parabola just touches the x-axis at this point; it doesn't cross. Because this is a positive quadratic, the parabola is always above the axis, other than at the one point where it just touches; the parabola is never below the axis.
The exercise is asking me for where the quadratic is less than zero, which is nowhere; and for where it is equal to zero, which is just the one point. So the "interval" is really just the point.
x = 2
Note that, had the above inequality been strict (that is, without the "or equal to" part), the inequality would have had no solution at all. Had the above inequality been "greater than or equal to", the solution would have been the entire number line; had it been a strict "greater than" inequaity, the solution would have been everything except 2.
The only other special cases for quadratic inequalities are when they have no (real-number) zeroes at all. This means that their parabolas are entirely on one side of the x-axis or the other, so the solution interval will be the entire number line, or nothing at all.
URL: https://www.purplemath.com/modules/ineqsolv2.htm
You can use the Mathway widget below to practice solving quadratic inequalities. Try the entered exercise, or type in your own exercise. Then click the button and select "Solve the inequality for x" to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




