Special Cases: All-x, No-x, or Exactly One x
Purplemath
When is "all x" or "no x" the solution to a quadratic inequality?
The solution to a quadratic inequality will be "all x" or "no x" only when the quadratic has no real-number zeroes; that is, when its associated parabola has no x-intercepts.
Content Continues Below
Advertisement
Whenever you have a quadratic inequality where the associated quadratic equation does not have real solutions (that is, where the associated parabola does not cross the x-axis), the solution to the inequality will either be "all x" or "no x", depending upon whether the parabola is on the side of the axis that you need.
If the parabola is always above the x-axis and the inequality is "greater than zero", then the solution will be "all x". If the parabola is above the x-axis and the inequality is "less than zero", then the solution will be "no x".
In the same way, if the parabola is always below the x-axis and the inequality is "greater than zero", then the solution will be "no x". If the parabola is below the x-axis and the inequality is "less than zero", then the solution will be "all x".
- Solve x2 + x + 1 > 0.
This quadratic is already isolated on one side of the inequality symbol, so I'll go straight to finding the zeroes:
Affiliate
Hmm... Since there is a negative inside the square root, there must not be any x-intercepts. That is, this quadratic must be either always above the x-axis or else always below because, without x-intercepts, it can never cross or touch the axis.
Since y = x2 + x + 1 is a positive quadratic, then its associated parabola is right-side-up; it opens upward. For the parabola not to cross the x-axis, it must be that the parabola is always above the axis, as I can see in the graph:
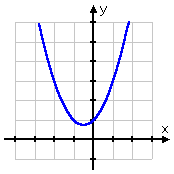
So where is y = x2 + x + 1 greater than zero (that is, where is it above the axis)? Everywhere!
Then my answer is:
all x
The above solution could also be stated as "all real numbers" or written as the interval (−∞, +∞).
- Solve x2 + x + 1 < 0.
This is the same quadratic as in the first example, except that now I'm looking for where the associated parabola is below the axis. I already know that there are no x-intercepts. Also, because this is a right-side-up parabola, I know that the graph is always above the axis. So where is y = x2 + x + 1 less than zero? Nowhere!
Then my answer is:
no x
The above solution could also be stated as "no solution" or as "the empty set", represented by the character "∅".
- Find the solution for x2 + 5 > 4x
To isolate the quadratic, I'll subtract the 4x over to the left-hand side, so my inequality is now:
x2 − 4x + 5 > 0
There are no factors of +5 that add to −4, so this quadratic does not factor. I'll plug it into the Quadratic Formula:
(If you haven't yet learned about complex numbers, being the ones that involve the imaginary number i, then you'd stop at the line with the square root of −1.)
Okay; so this quadratic has no *graphable* zeroes. The quadratic has two zeroes, but those zeroes are at imaginary x-values and are not graphable x-intercepts.
I know the shape of a parabola. If a parabola has no graphable x-intercepts, then the parabola is either always above the x-axis, or else always below the axis. This is a positive quadratic, so the parabola opens upward, and this parabola must always be above the axis.
This inequality is "greater than", so it's asking me where the quadratic is positive, and thus where its parabola is above the x-axis. Since the parabola is above the x-axis for all x, then the quadratic is positive for:
all x
I didn't bother doing the graph for this last exercise — though it probably wouldn't hurt to do a quick graphable check of my answer if this exercise were on a test. But as long as you know how parabolas behave, you can get your answer quickly by just picturing the graph in your head; there is no need to spend time doing "test points" on each of the intervals.
Content Continues Below
There is one fiddly case that you might not even have to deal with, but I'll cover it anyway, just in case your teacher likes tricky test problems.
What if the quadratic in the inequality only has one zero?
If the quadratic in an inequality has only one zero (that is, if the associated parabola has only one x-intercept), then the parabola only just touches the x-axis. If the parabola is on the wrong side of the x-axis for the inequality (such as being above the axis on a less-than inequality), then the solution will be just the one zero (if the inequality is or-equal-to) or else you'll have no solution at all (if the inequality is strict).
That probably sounded like a bunch of mumbo-jumbo, so let's see how it works in practice.
- Solve −x2 + 6x − 9 ≥ 0
The quadratic is already isolated, so I can go straight to finding the zeroes of y = −x2 + 6x − 9, the associated quadratic function:
−x2 + 6x − 9 = 0
x2 − 6x + 9 = 0
(x − 3)(x − 3) = 0
x = 3
So there is exactly one x-intercept. When I have only one intercept like this, the quadratic doesn't cross the axis, but instead just touches it, as I can see in the graph:
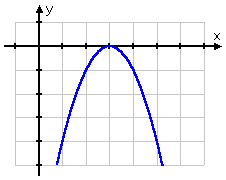
Affiliate
I need to find where y = −x2 + 6x − 9 is above the axis. But I know (and can verify from the above graph) that this quadratic only touches the axis from below; it is *on* the axis, but it is never above the axis.
However, this inequality is an "or equal to" inequality, so the "equal" part counts as part of the solution. Specifically, the one zero (that is, the one x-intercept) is part of the solution. In particular, since the parabola is below the axis, the one zero is actually the *only* solution. The graph only touches the axis (that is, it is only equal to zero); it never goes above (that is, it is never greater than zero).
So my solution is
x = 3
By the way, if you're supposed to write your solutions in set notation, a single-element set like this is written as {3} (those are curly-braces, not parentheses). This kind of set, containing only a single element, is called a "singleton" set.
In contrast to the previous exercise's solution, look at this exercise, which is *almost* the same:
- Solve −x2 + 6x − 9 > 0
In this case, they're asking me for where the graph is strictly above the axis. This is not an or-equal-to inequality, so the x-intercept doesn't count toward the solution set. The graph only touches the x-axis from below, it never crosses the axis, so it is never above the axis.
So the parabola is on the wrong side of the x-axis, and the one place where it touches the x-axis cannot be included in my solution. Then my answer is:
no solution
The answer can also be stated as "no x" or as "∅", which is the symbol for the empty set. (The symbol is not Greek; it comes from the Norwegian alphabet.)
As you've seen, when you are careful about finding the zeroes of the quadratic, and when you use your knowledge of the shape of quadratic graphs, solving quadratic inequalities can be pretty easy.
URL: https://www.purplemath.com/modules/ineqquad3.htm
You can use the Mathway widget below to practice solving quadratic inequalities. Try the entered exercise, or type in your own exercise. Then click the button and select "Solve the Inequality for x" to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




