Return to the Purplemath home page

 The Purplemath Forums
Helping students gain understanding
and self-confidence in algebra


powered by FreeFind

 

Return to the Lessons Index  | Do the Lessons in Order  |  Get "Purplemath on CD" for offline use  |  Print-friendly page

Graphing Quadratic Functions: Examples (page 3 of 4)

Sections: Introduction, The meaning of the leading coefficient / The vertex, Examples

  • Find the vertex and intercepts of y = 3x2 + x – 2 and graph; remember to label the vertex and the axis of symmetry.

    This is the same quadratic as in the last example. I already found the vertex when I worked the problem above. This time, I also need to find the intercepts before I do my graph. To find the y-intercept, I set x equal to zero and solve:

      y = 3(0)2 + (0) – 2 = 0 + 0 – 2 = –2

    Then the y-intercept is the point (0, –2). To find the x-intercept, I set y equal to zero, and solve:

      0 = 3x2 + x – 2
      0 = (3x – 2)(x + 1)
      3x – 2 = 0  or   x + 1 = 0
      x =  2/3   or  x = – 1

    Then the x-intercepts are at the points (–1, 0) and ( 2/3, 0).

    The axis of symmetry is halfway between the two x-intercepts at (–1, 0) and at ( 2/3 , 0); using this, I can confirm the answer from the previous page:

      (–1 + 2/3) / 2 = (–1/3) / 2 = –1/6

    The complete answer is a listing of the vertex, the axis of symmetry, and all three intercepts, along with a nice neat graph:

       

    The vertex is at ( –1/6 , –25/12 ), the axis of symmetry is the line x = –1/6 , and the intercepts are at (0, –2), (–1, 0), and ( 2/3, 0).

     

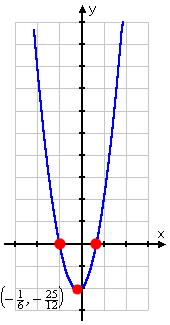
    graph of y = 3x^2 + x - 2 with vertex and intercepts marked.
     
  • Find the intercepts, the axis of symmetry, and vertex of y = x2 – x – 12.

    To find the y-intercept, I set x equal to 0 and solve:

      y = (0)2 – (0) – 12 = 0 – 0 – 12 = –12

    To find the x-intercept, I set y equal to 0 and solve:

      0 = x2 – x – 12

      0 = (x – 4)(x + 3)

      x = 4  or  x = –3

    To find the vertex, I look at the coefficients: a = 1 and b = –1. Plugging into the formula, I get:

      h = –(–1)/2(1) = 1/2 = 0.5

    To find k, I plug h = 1/2 in for x inside y = x2 – x – 12, and simplify:

      k = (1/2)2 – (1/2) – 12 = 1/4 – 1/2 – 12 =  –12.25

    Once I have the vertex, it's easy to write down the axis of symmetry: x = 0.5. Now I'll find some additional plot points, to fill in the graph:

      T-chart

    For my own convenience, I picked x-values that were centered around the x-coordinate of the vertex. Now I can plot the parabola:   Copyright © Elizabeth Stapel 2002-2011 All Rights Reserved

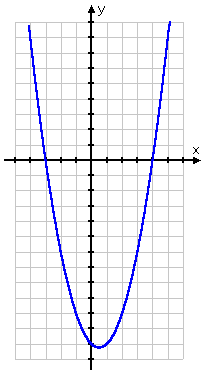
      graph of y = x^2 - x - 12

    The vertex is at the point (0.5, –12.25),
       the axis of symmetry is the line     x = 0.5,
              and the intercepts are at the points (0, –12),  (–3, 0), and (4, 0).

<< Previous  Top  |  1 | 2 | 3 | 4  |  Return to Index  Next >>

Cite this article as:

Stapel, Elizabeth. "Graphing Quadratic Functions: Examples." Purplemath. Available from
    http://www.purplemath.com/modules/grphquad3.htm. Accessed
 

 

Purplemath:
  Linking to this site
  Printing pages
  Donating
  School licensing

Reviews of
Internet Sites:
   Free Help
   Practice
   Et Cetera

The "Homework
   Guidelines"

Study Skills Survey

Tutoring from Purplemath
Find a local math tutor

This lesson may be printed out for your personal use.

Content copyright protected by Copyscape website plagiarism search

  Copyright © 2002-2012  Elizabeth Stapel   |   About   |   Terms of Use

 

 Feedback   |   Error?