Worked Examples of Graphing Translated Exponential Functions
Purplemath
Many, if not most, of the graphing you'll be doing of exponential functions will be variations on the regular shape of an exponential curve. But a minus sign on the variable in the exponent, or a base whose value is between zero and one (*not* inclusive), can flatten the curve somewhat, or flip it around backwards (so the graph comes screaming down from on high on the left-hand side, while riding the x-axis on the right-hand side), etc.
Content Continues Below
You will also likely have functions whose graphs have been shifted up or down a bit.
These are all transformations or translations in the plane. Which is a fancy way of saying that there are quite a few ways to draw essentially the same graph.
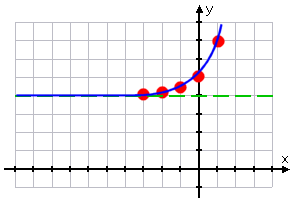
- Graph y = 2x + 4
This is the standard exponential, except that the "+ 4" pushes the graph up so it is four units higher than usual.
First I compute some points:
Then I plot those points:
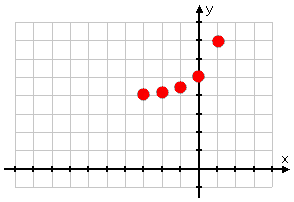
Students, when they're just starting out with exponential graphs, very often only compute y-values for a few x-values that are close to zero, and sometimes they'll only compute values for x-values that are zero or positive. Then either they have no idea where the graph goes on the left-hand side, and just leave it hanging there:
This graph is WRONG!
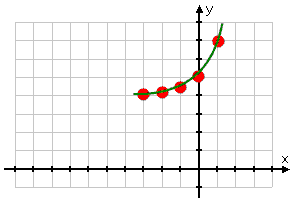
...or else they take the graph down to the x-axis, as is usual for the standard exponential graph:
This graph is also WRONG!
Affiliate
But y = 2x + 4 isn't the standard exponential graph; it is the standard exponential graph shifted upward by four units. When x is negative, y = 2x + 4 won't be very close to zero; instead, it will be very close to 4, because the values will be "a teensy-tiny little number, plus four", which works out to be a teensy-tiny bit more than four.
To help me with my graph, and to indicate that I know that y = 2x + 4 never goes below (or even touches, for that matter) the line y = 4, I will drawn a dashed line at y = 4:
Drawing my dashed line:
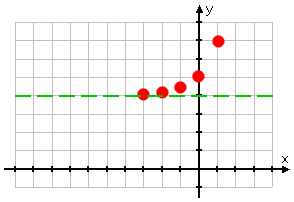
This dashed-in line, indicating where the graph goes as x heads off to the left, is called a "horizontal asymptote", or just an "asymptote". It is not required that you draw it in, but it can be helpful for graphing, and can point out to your teacher on the test that you do know what you're doing.
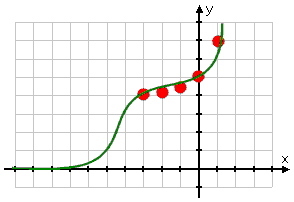
Now that I have my plotted points and my asymptote, I'll draw my exponential curve:
Graph of y = 2x + 4
Content Continues Below
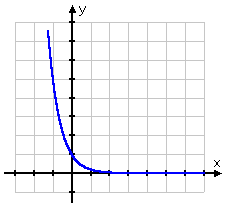
- Graph y = 5−x
I need to remember that the "minus" exponent reverses the location (along the x-axis) in which the power on 5 is negative. When the x-values are negative (that is, when I'm on the left-hand side of the graph), the value of −x will be positive, so the graph will grow quickly on the left-hand side.
On the other hand, when the x-values are positive (that is, on the right-hand side of the graph), then the corresponding values of −x will be negative. This means that the graph will stay very close to the x-axis as the graph goes off to the right.
In other words, the standard values are reversed:
Then y = 5−x graphs as:
Affiliate
Advertisement
Any graph that looks like the one directly above (that is, any graph that is big on the left and crawling along the x-axis on the right) displays exponential decay, rather than exponential growth. For a graph to display exponential decay, either the exponent is "minus" or else the base is between 0 and 1. You should expect to need to be able to identify the type of exponential equation (that is, growth versus decay) from the graph.
The worked example on the previous page, and the first exercise above, displayed exponential growth; the example directly above displays exponential decay. The graph for the following exercise displays exponential growth again.
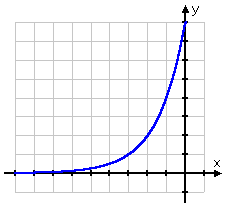
- Graph y = 2(x + 3)
This equation is not the same as y = 2x + 3. In 2x + 3, the standard exponential is shifted up three units. In this case, the shift is inside the exponent. Instead of the + 3 shifting the 2x up by three, the + 3 shifts the 2x over sideways by three. The only question is: shifts sideways which way, left or right?
The way I keep it straight is to consider one of the basic points on any exponential. When the power is zero, the exponential is 1. For 2(x + 3), when is the power zero? It will be zero when x + 3 = 0, so x = −3. That is, the basic plot point (0, 1) has been shifted to the point (−3, 1), so the graph has been shifted three points to the left:
There is no upward or downward shift for this graph, so the left-hand side will get and stay close to the x-axis as the graph moves off to the left. On the right-hand side, the graph will shoot up through the top.
So my graph looks like this:
URL: https://www.purplemath.com/modules/graphexp3.htm
You can use the Mathway widget below to practice graphing exponential functions what have been transformed (that is, moved around the axis system). Try the entered exercise, or type in your own exercise. Then click the button and select "Graph" to compare your answer to Mathway's. (Or skip the widget and continue with the lesson.)
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




