Evaluation: Functions

The Purplemath Forums
Helping students gain understanding
and self-confidence in algebra

Return to the Lessons Index | Do the Lessons in Order | Get "Purplemath on CD" for offline use | Print-friendly page

Evaluation: Evaluating Expressions,
Polynomials, and Functions (page 2 of 2)

Sections: Evaluating Expressions and Polynomials, Evaluating Functions

Evaluate y = 4x – 3 at x = 0.

y = 4(0) – 3 = 0 – 3 = –3

This means that the point (0, –3) is on the line.

Evaluate y = 4x – 3 at x = 3.

y = 4(3) – 3 = 12 – 3 = 9

Then (3, 9) is on the line.

By the way, evaluating the same equation at three or more points like this, and getting a list of points, is how you plot points and graph equations.

In this case, the points from the evaluating (including the point from the previous page) are: (–1, –7), (0, –3), and (3, 9).

Then the graph looks like the drawing at the right:

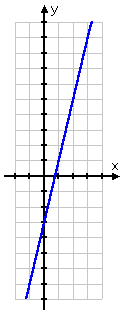
You can verify from the picture that the three points I found are indeed on the graph.

y = 4x - 3

You will also need eventually to evaluate functions.

For the following exercises, let .

Evaluate f(–3).

To evaluate a function, I do just what I did above: I plug in the given value for x. Here, I am supposed to evaluate at the value x = –3. The notation is different, but "f(–3)" means exactly the same thing as "evaluate at x = –3"!

f(-3) = 4

Note how I used parentheses. It is very easy to mess up the minus signs if you're not careful and use lots of parentheses. Take the time to be careful!

	ADVERTISEMENT

Evaluate f(3).

f(3) = 4

Evaluate f(–1).

f(-1) = sqrt(24)

Note that I gave the answer in two formats: the "exact" form (with the radical in it) and the "approximate" form (with the wiggly "equals"). Usually you will be expected to evaluate exactly; that is, it will usually be correct to leave the answer in a messy form (with a radical, or a fraction, or with pi in it [instead of rounding to 3.14], etc). However, there are times when the approximate form is better. Often, word problems need an answer that can be applied in "real life". For instance, "square root of 24 meters" isn't very useful when you're trying to figure out to what length to cut a board, but "about 4.9 meters" is perfectly useful, and probably quite accurate enough for whatever you're building. You will also need to approximate for when you're graphing. For instance, I would have no idea where to plot the square root of 24, but I know right where to draw the line for 4.9.

By the way, you graph functions just like you graph other equations: by evaluating the function at a few values of x, drawing the points, and connecting the dots. (This is exactly what a graphing calculator does, by the way.) The graph of the function used in the three examples above looks like this:

f(x) = sqrt(25 - x^2)

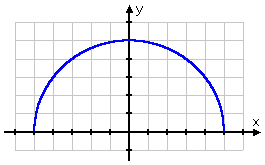
Just remember: "evaluate" means "plug-n-chug". Be careful with the subtractions, negatives, and exponents (by using parentheses appropriately). Don't try to do too much at once; don't skip steps, don't try to do three steps at once, and don't try to do everything in your head. Take your time, and evaluation problems should work out fine!

<< Previous Top | 1 | 2 | Return to Index

Cite this article as:

Stapel, Elizabeth. "Evaluation: Functions." Purplemath. Available from
http://www.purplemath.com/modules/pageaddy.htm. Accessed

Purplemath:
  Linking to this site
  Printing pages
  Donating
  School licensing

Reviews of
Internet Sites:
   Free Help
   Practice
   Et Cetera

The "Homework
Guidelines"

Study Skills Survey

Tutoring from Purplemath
Find a local math tutor

This lesson may be printed out for your personal use.

Copyright © 2000-2012 Elizabeth Stapel \| About \| Terms of Use		Feedback \| Error?