Why and How the Division Method Works
Purplemath
Why does the division method work for converting decimal numbers to other bases?
In repeatedly dividing the decimal number by the base of the non-decimal number, we are implicitly expanding the number by powers of that non-decimal number. The remainders tell us how far off we are from that power of the non-decimal number.
Content Continues Below
To see this in action, let's consider the binary case. We had been converting the base-10 number 357 into binary form:
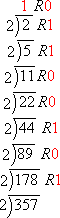
Advertisement
When you divide a number by two, the remainder will be either a zero or a one. If the remainder is 0, then the base-ten number must have been even (that is, a multiple of two), so there will be no ones, and therefore the right-most digit will be "0". If the remainder is 1, then the base-ten number must have been odd (that is, one more than a multiple of two), so there will be a "1" as the right-most digit in the units column.
Affiliate
Now divide again by two. If the remainder is zero, then, after getting rid of any extra 1 (from being an odd number), the number that was left must be a multiple of four, so there won't be any 2 left over. Otherwise, there was a multiple of two left over, so there will be a 1 in the twos column.
Continue in like manner. Each time you divide, you're asking "Does the original number contain a multiple of this power of two?", and the remainder is either telling you "yes" (with a "0") or "no" (with a "1").
Here's what it looks like in math (rather than in words, as above):
357
2×178 + 1×20
178×21 + 1×20
(89×21 + 0)×21 + 1×20
89×22 + 0×21+ 1×20
(44×21 + 1×20)×22 + 0×21 + 1×20
44×23 + 1×22 + 0×21 + 1×20
(22×21 + 0)×23 + 1×22 + 0×21 + 1×20
22×24 + 0×23 + 1×22 + 0×21 + 1×20
(11×21 + 0×20)×24 + 0×23 + 1×22 + 0×21 + 1×20
11×25 + 0×24 + 0×23 + 1×22 + 0×21 + 1×20
(5×21 + 1×20)×25 + 0×24 + 0×23 + 1×22 + 0×21 + 1×20
5×26 + 1×25 + 0×24 + 0×23 + 1×22 + 0×21 + 1×20
(2×21 + 1×20)×26 + 1×25 + 0×24 + 0×23 + 1×22 + 0×21 + 1×20
2×27 + 1×26 + 1×25 + 0×24 + 0×23 + 1×22 + 0×21 + 1×20
(1×21 + 0)×27 + 1×26 + 1×25 + 1×24 + 0×23 + 1×22 + 0×21 + 1×20
1×28 + 0×27 + 1×26 + 1×25 + 0×24 + 0×23 + 1×22 + 0×21 + 1×20
Recall that the binary form of 357 that we found by dividing was 1011001012. Now look at the coefficients of the powers of 2 in the last line above:
1×28 + 0×27 + 1×26 + 1×25 + 0×24 + 0×23 + 1×22 + 0×21 + 1×20
The coefficients on this expansion match the binary's digits. (But doing the divisions is much faster and easier.)
Affiliate
This reasoning carries through with other bases. If, say, you're converting to base eleven and you divide by 11, the remainder will tell you how many more than a multiple of eleven the given number is. Since this remainder value must be between 0 (if the number is an exact multiple of eleven) and 10 (one less than a multiple of eleven), then the digits in a base-eleven number will never contain one single solitary digit for "eleven".
Note: For bases larger than 10, the numbers must include extra "numerals" — in the form of letters — to account for the fact that we, using base-10 numbers, have no digits for the other digits required in these number bases. This is why, in hexadecimal number, you'll see the capital letters A, B, C, D, E, and F. These letters are the digits representing the numbers 10, 11, 12, 13, 14, and 15. For base-11, you'd see the digit A, which stands for 10.
URL: https://www.purplemath.com/modules/base_why.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




