Slant (Oblique) Asymptotes
Purplemath
In the previous section, covering horizontal asymptotes, we learned how to deal with rational functions where the degree of the numerator was equal to or less than that of the denominator.
But what happens if the degree is greater in the numerator than in the denominator?
Content Continues Below
Recall that, when the degree of the denominator was bigger than that of the numerator, we saw that the value in the denominator got so much bigger, so quickly, that it was so much stronger that it pulled the functional value to zero, giving us a horizontal asymptote of the x-axis.
Reasonably, then, if the numerator has a power that is larger than that of the denominator, then the value of the numerator ought to be stronger, and ought to pull the graph away from the x-axis; that is, it ought to pull the graph away from the line y = 0 and away from any other fixed y-value.
To investigate this, let's look at the following function:
For reasons that will shortly become clear, I'm going to apply long polynomial division to this rational expression. My work looks like this:
Across the top is the quotient, being the linear polynomial expression −3x − 3. At the bottom is the remainder. This means that, via long division, I can convert the original rational function they gave me into something akin to what would be mixed-number format in numerical values:
This is the exact same function. All I've done is rearrange it a bit. Why? You're about to see.
First, take a look at the graph of the rational function they gave us:
![graph of y = [−3x^2 + 2] / [x − 1]](rational/asympt20.gif)
The parts in the middle, where the line goes pretty much straight up though the top and then comes pretty much straight up from the bottom, indicate where there's a vertical asymptote (at x = 1). But what about the slanty parts, that seem to kind of line up with each other?
Thinking back to the results of my long division, we know what the graph of y = −3x − 3 looks like; it's a decreasing straight line that crosses the y-axis at −3, having a slope of m = −3.
Now take a look at this second graph of the same rational function, but with the line y = −3x − 3 superimposed on it:
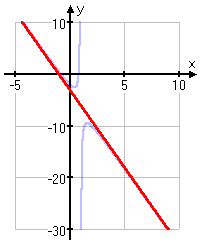
As you can see, apart from the middle of the plot near the origin (that is, apart from when the graph is close to the vertical asymptote), the graph hugs the line y = −3x − 3. Because of this "skinnying along the line" behavior of the graph, the line y = −3x − 3 is an asymptote.
Clearly, though, it's not a horizontal asymptote. Instead, because this asymptote is slanted or, in fancy terminology, "oblique", this is called a slant (or oblique) asymptote.
Affiliate
The graph above illustrates the fact that, if the degree of the numerator is exactly one more than the degree of the denominator (so that the polynomial fraction is an "improper" fraction), then the graph of the rational function will be, roughly, a slanty straight line with some fiddly bits in the middle.
Why does it work like this? Because of the how the long division works out. The degree of the numerator is one more than the degree of the denominator, so the long division will give you a degree-1 (that is, a linear) polynomial part (in other words, something of the form mx + b) and a "proper" fractional part.
We already know that, off to the sides, the fractional part will quickly go to the x-axis; that is, its value will quickly get, and stay, close to zero. So, off to the sides, the graph will pretty much boil down to (the linear polynomial part) plus (zero). In other words, most of the graph will be approximately equal to the linear polynomial part.
Because the graph will be nearly equal to this slanted straight-line equivalent, the asymptote for this sort of rational function is called a slant (or "oblique") asymptote. The equation for the slant asymptote is the polynomial part of the rational that you get after doing the long division.
(By the way, this relationship — between an improper rational function, its associated polynomial, and its graph — holds true regardless of the difference in the degrees of the numerator and denominator. However, in most textbooks, they only have you work with a degree-difference of one.)
Content Continues Below
To summarize:
What is a slant (or oblique) asymptote?
Suppose a rational function has a numerator whose degree is exactly 1 greater than the denominator's degree. The slant (or oblique) asymptote for that rational function is a straight (but not horizontal or vertical) line that shows where the graph goes, off to the sides.
How do you find the slant (or oblique) asymptote?
To find the slant asymptote, do the long division of the numerator by the denominator. The result will be a degree-2 polynomial part (across the top of the long division) and a proper fractional part (formed by dividing the remainder by the denominattor). The linear polynomial, when set equal to y, is the slant asymptote.
What is the difference between slant, horizontal, and vertical asymptotes?
- Vertical asymptotes are caused by zeroes of the denominator; they indicate where the graph must *never* go, as this would cause division by zero. As a result, they can *never* be touched or crossed.
- Horizontal asymptotes are caused by the numerator having a degree that is smaller than, or equal to, the degree of the denominator; they indicate where the graph will be when it's off to the sides (away from vertical asymptotes, etc). Horizontal asymptotes can be touched and/or crossed.
- Slant asymptotes are caused by the numerator having a degree that is 1 greater than that of the denominator; they indicate where the graph will be when it's off to the sides. Slant asymptotes can be touched and/or crossed.
- Find the slant asymptote of the following function:
To find the slant asymptote, I need to do the long division:
I need to remember that the slant asymptote is the polynomial part of the answer (that is, the asymptote is the part across the top of the division, set equal to y), not the remainder (that is, not the last value at the bottom). Then my answer is:
slant asymptote: y = x + 5
Affiliate
- Find the slant asymptote of the following function:
They've tried to trip me up here! They omitted a linear term in the polynomial on top, and they put the terms in the wrong order underneath. When I'm doing my long division, I'll need to be careful to include the missing linear term in the numerator, and I'll need to keep track of the signs when I reverse the terms in the denominator.
The slant asymptote is the polynomial part of the answer; I can ignore the remainder. So my answer is:
slant asymptote: y = −2x − 4
(If you're not comfortable with the long-division part of these exercises, then go back and review now!)
A note for the curious regarding the horizontal and slant asymptote rules. Otherwise, continue on to the worked examples.
URL: https://www.purplemath.com/modules/asymtote3.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()



